2.2 Quadratische Funktionen

Die allgemeine Form der quadratischen Funktion lautet:

f(x) = ax2 + bx + c

Funktionsverlauf

Die Graphen quadratischer Funktionen zeichnen sog. Parabeln. Einige Beispiele:

Der Koeffizient von x², also a, bestimmt die Form der Parabel. Bei einem positivem Wert von a ist die Parabel nach oben, bei einem negativen Wert nach unten geöffnet.

Je größer |a| gewählt wird, desto enger wird die Parabel. Analog wird die Form der Parabel für ein kleineres |a| "dicker":

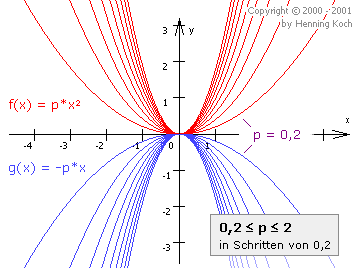Zeichnen des Funktionsgraphen

Die oben aufgeführte, allgemeine Form der quadratischen Funktion lässt sich nur schwer zeichnen, deswegen formen wir sie mittels quadratischer Ergänzung in diese einfacher zu benutzende Form um:

f(x) = a(x – x0)2 + d

Das Ziel bei der quadratischen Ergänzung ist es, den Term so umzuformen, dass man ihn teilweise mit einer binomischen Formel ersetzen kann. Ein Rechenbeispiel:

f(x) = 2x2 + 6x + 2; a ausklammern: f(x) = 2(x2 + 3x + 1); Das gemischte Glied 3x zerlegen: f(x) = 2(x2 + 2·1,5·x + 1); 1,52 addieren und wieder subtrahieren: f(x) = 2(x2 + 2·1,5·x + 1,52 - 1,52 + 1); Binomische Formel a2 + 2ab + b2 = (a + b)2 anwenden: f(x) = 2(x2 + 2·1,5·x + 1,52 - 1,25); f(x) = 2((x + 1,5)2 - 1,25); Term vereinfachen: f(x) = 2(x + 1,5)2 - 2,5;

Der Vorteil dieser Form ist, dass man sofort die Position des Scheitelpunktes der Parabel S ablesen kann:

S(x0|d)

In diesem Beispiel ist S(-1,5|-2,5). Vom Scheitelpunkt aus geht man nun, ähnlich wie bei einer Wertetabelle, um ½, 1, ¾, 2, etc. nach rechts und um das Quadrat des jeweiligen Wertes multipliziert mit a nach oben:

Hat man genug Stützpunkte angezeichnet, kann man die rechte Hälfte der Parabel anskizzieren. Die linke Seite der Parabel ist einfach die an einer Parallele zur Y-Achse durch S gespiegelte rechte, bereits gezeichnete Seite:

Nullstellen

Eine quadratische Funktion hat je nach Lage des Scheitelpunktes S und dem Vorzeichen von a eine, zwei oder gar keine Nullstellen.

Zur Berechnung der Nullstellen setzt man f(x) = 0 und löst die Gleichung mittels der quadratischen Lösungsformel:

ax2 + bx + c = 0;     x1/2 =      –b ±       b2 – 4ac         2a

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
2.3 Höhergradige Polynome