3.7 Verhalten im Unendlichen

Wie wir aus Kapitel 2.3.9 wissen, streben ganzrationale Funktionen für große x immer gegen + oder -. Gebrochenrationale Funktionen hingegen können auch ganz anderes Verhalten im Unendlichen zeigen, wie man an diesen Beispielen sieht:

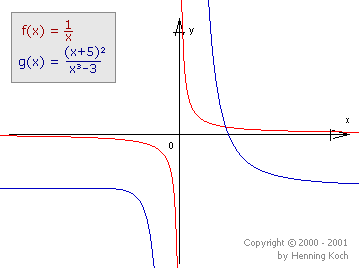Tatsächlich kann eine gebrochenrationale Funktion, abhängig von den Graden des Zähler- und Nennerpolynoms, ganz verschiedene Verhalten im Unendlichen zeigen.

Asymptoten und Grenzkurven

Bei einer gebrochenrationalen Funktion

f(x) =      g(x)     h(x)

sei z der Grad des Zählerpolynoms g(x) und n der Grad des Nennerpolyoms h(x).

1. z < n
   

   Da das Nennerpolynom für große X-Werte schneller wächst als das Zählerpolynoms, nähert sich die Funktion für x ± an die X-Achse an. Man sagt auch die X-Achse ist waagrechte Asymptote der Funktion (Senkrechte Asymptoten haben wir bereits kennengelernt). Ein Beispiel:

   In der Rechnung schreibt man das so:

   f(x) =      x2 + 4     x3 – x2 – 3       =      0

   Das Zeichen "" spricht man "Limes von x gegen Unendlich".

2. z = n
   

   Zähler und Nenner wachsen für große X-Werte etwa gleich schnell, womit der Bruch sich einem konstantem Wert nähert. Die Funktion hat also eine waagrechte Asymptote, eine Parallele zur X-Achse. Durch Polynomdivision können wir berechnen, an welchem Y-Wert entlang die Asymptote verläuft:

   f(x) =      x2 – 1     4x2 – x       =      =      1     4      –      1 + 0,25x     4x2 – x       =      (Der zweite Bruch ist eine Funktion mit z < n und wird damit zu 0!)     =      1     4      =     0,25

   Die Asymptote ist also eine Parallele zur X-Achse bei y = 0,25:

   Noch einfacher läßt sich dieser Wert (0,25) berechnen, indem man einfach den Koeffizienten des höchsten Glieds im Zähler durch den Koeffizienten des höchsten Glieds im Nenner teilt:

   f(x) =      1x2 – 1     4x2 – x       =       1     4      =     0,25

3. z = n + 1
   

   Da der Zähler für große Werte "um ein x" schneller wächst als der Zähler, nähert sich der Bruch einer Geraden der Form a(x) = mx + t an. Die Asymptote der Funktion ist also eine Gerade. Durch Polynomdivision können wir die Geradengleichung der Asymptote bestimmen:

   f(x) =      x3 + x2     –2x2 + 10       =  –      1     2      x –      1     2      +      5x + 5     –2x2 + 10      ;     Wir erkennen das letzte Glied des Termes, das für unendlich große x zu Null wird:     –      1     2      x –      1     2      +      5x + 5     –2x2 + 10      =      1     2      x –      1     2      =     –0,5x – 0,5

   Die Geradengleichung der Asymptoten ist also a(x) = -0,5x - 0,5.

4. z > n + 1
   

   Analog nähert sich eine solche Funktion für große X-Werte einem Polynom vom Grade z-n an: Durch Polynomdivision können wir die Funktionsgleichung dieses "Grenzpolynoms" bestimmen:

   f(x) =      x3 + 2x2 – 2     x + 1       =  x2 + x – 1 –      1     x + 1      ;     Wir erkennen das Glied des Termes, das für unendlich große x zu Null wird:     x2 + x – 1 –      1     x + 1       =      x2 + x – 1

   Die Gleichung des Polynoms lautet also p(x) = x² + x - 1:

Anmerkung zu den Grenzkurven

Natürlich ist es für sehr große X-Werte nicht mehr sonderlich relevant, ob die Gleichung der Grenzkurve nun p(x) = x² + x - 1 oder p(x) = x² - x - 1 lautet. Wirklich ausschlaggebend für das Vorzeichen des Funktionswertes im Unendlichen ist hier, wie in Kapitel 2.3.9 besprochen, nur noch das höchstgradige Glied des Grenzkurventerms, in diesem Falle x².

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
3.8 Beschränktheit und globale Extremwerte