4.1 Grenzwert für x gegen x₀

Diese Art von Grenzwertrechnung benutzt man unter anderem, um sich bei Funktionen an Werte anzunähern, die eigentlich gar nicht definiert sind. Dazu geht man von beiden Seiten an die "verbotene" Stelle immer näher heran, z.B. bei einer Definitionslücke:

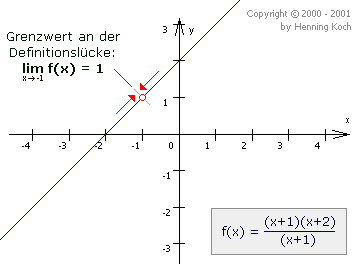Man muß unbedingt verstanden haben, dass f(x) = 1 nicht das Gleiche ist wie f(-1)! Das ist nach wie vor nicht definiert! Stattdessen ist f(x) = 1 ein Wert von f(x), der unendlich nahe an x = 1 dranliegt.

Zur Schreibweise bei der Rechnung:

f(x) =      (x+1)(x+2)     (x+1)      =     x+2 =     1

Wenn man bei komplizierteren Funktionstermen mit diesem direkten Ansatz nicht weiterkommt (z.B. weil der Nenner partout nicht 0 werden will), kann man auch die sog. h-Methode anwenden:

f(–1±h) =      (–1+1±h)(–1±h+2)     (–1±h+1)      =     –1±h+2 =     1

Grenzwertrechnung kann, wie an diesem Beispiel gesehen, oft sehr trivial und offensichtlich sein, dennoch ist es nötig, die Idee dahinter verstanden zu haben.

Einseitige Grenzwerte

Besonders bei abschnittsweise definierten Funktionen kommt es vor, dass man zwar von zwei Seiten an einen Punkt herangehen kann, aber zwei verschiedene Werte herausbekommt:

Man schreibt:

• f(x): linksseitiger Grenzwert von f(x)

• f(x): rechtsseitiger Grenzwert von f(x)

Wie man an dem Beispiel aus dem Bild gesehen hat, muß man sich manchmal an eine Stelle von verschiedenen Seiten auch über verschiedene Funktionen herantasten:

f(x) =     x+1   für x < 0     x–1   für x > 0         f(x) = x+1 =     1       (wir gehen von links an x = 0 heran)     f(x) = x–1 =     –1       (wir gehen von rechts an x = 0 heran)

Der Grenzwert f(x) existiert nur, wenn beide einseitigen Grenzwerte übereinstimmen, also f(x) = f(x) ist.

Kompliziertere Grenzwertübergänge

Oft muss man erst einmal dafür sorgen, dass beim Grenzwertübergang der Nenner eines Bruchterms nicht 0 wird. Dabei hilft häufig die Anwendung einer binomischen Formel:

x2 – 9     x – 3      =      (x + 3)·(x–3)     x – 3      = x + 3 =     6

Kann man keine binomische Formel anwenden, hilft oft nur die h-Methode. Dabei berechnet man f(x₀+h) und löst den Term vollständig auf:

x3 – 1     x2 – 1      =      (1+h)3 – 1     (1+h)2 – 1      =     =      h3 + 3h2 + 3h + 1 – 1     h2 + 2h + 1 – 1      =     =      h(h2 + 3h + 3)     h(h + 2)      =     =      h2 + 3h + 3     h + 2      =      3     2      =     1,5

Es sei angemerkt, dass man vor allem bei zusammengesetzten Funktionen auch bei der h-Methode manchmal von zwei Seiten, über zwei verschiedene Funktionen an eine Stelle herangehen muss. D.h. man hat dann wieder zwei Rechnungen, eine für f(x₀-h) (linksseitiger Grenzwert) und eine für f(x₀-h) (rechtsseitiger Grenzwert).

Grenzwertrechnung ist keine Magie!

Um bei der Grenzwertrechnung eines reellen Wert herauszubekommen, muss die betrachtete Funktion auch entsprechend beschaffen sein. Die Grenzwertrechnung ändert nichts an den Funktionswerten selbst. Hat die Funktion k(x) beispielsweise bei x₀ eine Unendlichkeitsstelle, so wird auch bei der Berechnung von k(x) das Ergebnis , bzw. - herauskommen. Man darf das allerdings nicht auf den ersten Blick entscheiden, sondern muss erst versuchen, den Bruch in eine geeignete Form zu bringen (z.b. eben durch die h-Methode).

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
4.2 Stetigkeit