4.3 Ableitung und Differenzierbarkeit

Will man eine abschnittsweise definierte Funktion ableiten, muss man jede der Teilfunktionen ableiten. Es gilt dann, außer an den Grenzen der einzelnen Teilfunktionen, je nach X-Wert die Ableitung der Funktion der entsprechenden Definitionsmenge:

Differenzierbarkeit

Im Gegensatz zu ganzrationalen und gebrochenrationalen Funktionen können wir abschnittsweise definierte Funktionen selten auf ganz ableiten. Das Problem sind die Grenzen, die Übergangspunkte zwischen den einzelnen Teilfunktionen:

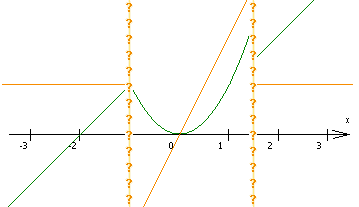Um feststellen, ob man die Funktion an dieses Grenzstellen überhaupt ableiten kann, müssen wir eine Ableitung für eine einzelne Stelle x₀ bilden:

f'(x0) =      f(x0) – f(x)     x – x0      =      f(x0) – f(x)     x – x0

Existiert der Grenzwert, so nennt man ihn den Differentialquotienten von f(x) an der Stelle x₀. Weil es für die Rechnung meist einfacher ist, verwendet man oft die gleichwertige "h-Form":

f'(x0) =      f(x0–h) – f(x0)     –h      =      f(x0+h) – f(x0)     h

Ist diese Gleichung erfüllt, so kann man die Steigung von f(x) an der Stelle x₀ errechnen. Man nennt dann f(x) an der Stelle x₀ differenzierbar. Differenzieren und Ableiten sind, wie wir wissen, zwei Worte für die gleiche Sache.

Ist eine Funktion an einer Stelle x₀ nicht differenzierbar, können wir dort nicht wie gewohnt Aussagen über lokale Maxima, Wendepunkte, etc. machen. Ist die Funktion bei x₀ nicht differenzierbar, jedoch stetig, so kann sie dort eventuell einen lokalen Extremwert besitzen. Diese sog. "Randextrema" behandeln wir in Kapitel 4.4.

Differenzierbarket rationaler Funktionen

Rationale Funktionen (nicht abschnittsweise definierte Funktionen) sind immer auf ihrem Definitionsbereich differenzierbar, da alle auf nicht differenzierbaren Stellen (Unendlichkeitsstellen, Definitionslücken) nicht in enthalten sind.

Rechenbeispiel

Wir wollen die Funktion f(x) auf ihre Differenzierbarkeit in hin untersuchen. Wie immer muss man beim Untersuchen der Grenzstellen stets sehr genau darauf achten, in welche Teilfunktion man einen X-Wert einsetzen muss:

f(x) =     x + 2   für x < –1     x2   für x –1         Die Teilfunktionen sind rationale Funktionen und damit auf ihrem jeweiligen Definitionsbereich in sich differenzierbar. Uns interessieren aber die Grenzstellen zwischen den Teilfunktionen: Lässt sich f(x) bei x0 = –1 ableiten? Zuerst gehen wir von links an x0 heran:          f(–1–h) – f(–1)     –h      =     =      (–1–h+2) – (–1)2     –h      =      –h     –h      =     1         Jetzt berechnen wir den Grenzwert von der rechten Seite aus:          f(–1+h) – f(–1)     h      =      (–1+h)2 – (–1)2     h      =     =      1 + h2 – 2h – 1     h      = =      h(h – 2)     h      =     = h – 2 =     –2         Die Funktion f(x) ist an der Stelle x0 nicht differenzierbar, da 1 –2!

Stetigkeit und Differenzierbarkeit

Es gibt einen Zusammenhang zwischen Stetigkeit und Differenzierbarkeit einer Funktion:

• Differenzierbarkeit bei x₀ Stetigkeit bei x₀
• keine Stetigkeit bei x₀ keine Differenzierbarkeit bei x₀

Ist also f(x) in einem Interval nicht stetig, ist f(x) in diesem Interval auch nicht vollständig differenzierbar. Man muss sich aber einprägen, dass das Umgekehrte nicht gilt:

• Stetigkeit bei x₀ Differenzierbarkeit bei x₀

Man sieht das besonders deutlich bei den abschnittsweise definierten Funktionen, die auch bei gegebener Stetigkeit nur sehr selten vollständig differenzierbar sind.

Ableitung in einem Intervall

Ist f(x) nur für ein Intervall definiert, so ist das Intervall, für das f'(x) definiert ist, immer ausschließend. Die Intervall-Grenzen sind nie im Intervall von f'(x) enthalten:

= [a;b] = ]a;b[ = ]a;b] = ]a;b[ = [a;b[ = ]a;b[ = ]a;b[ = ]a;b[

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
4.4 Randextrema