Vorzeichenverlauf des Graphen - Rationale Funktionen

2.3.2 Vorzeichenverlauf des Graphen

Im Gegensatz zu den gebrochenrationalen Funktionen hängt der Vorzeichenverlauf bei Graphen ganzrationaler Funktionen ausschließlich von den Nullstellen der Funktion ab.

Vorzeichenwechsel des Graphens

Wie man bereits an der einfachen Funktion f(x) = x² sehen kann, muss an einer Nullstelle nicht zwingen ein Vorzeichenwechsel des Graphens erfolgen:

Tatsächlich gibt es nur einen Vorzeichenwechsel, wenn eine Nullstelle ungeraden Grades vorliegt. Liegt eine doppelte, vierfache, etc. Nullstelle vor, wie bei f(x) = x², berührt der Graph die X-Achse zwar an dieser Stelle, durchschneidet sie aber nicht.

Die Methode des "Felderabstreichens"

Hat man eine Funktion gegeben und mit dem Zerlegungssatz soweit wie möglich zerlegt, kann man sich bereits einen ungefähren Eindruck vom Verlauf des Graphens machen, indem man Felder abstreicht (ausschraffiert), in denen der Graph auf keinen Fall verlaufen kann.

Als Beispiel nehmen wir die Funktion

f(x) = x⁴ – 4x³ – 3x² + 10x + 8

Wir zerlegen durch Polynomdivision die Funktion in ihre Linearfaktoren und erhalten:

f(x) = (x–2)·(x+1)·(x+1)·(x–4)

Das Vorzeichen von f(x) in einem bestimmten Abschnitt ist das Produkt der Vorzeichen der einzelnen Faktoren der zerlegten Funktion. Wir schreiben also die Faktoren mit ihren jeweiligen Vorzeichen zwischen den Nullstellen in eine Tabelle, und bekommen durch Multiplikation den Vorzeichenverlauf von f(x):

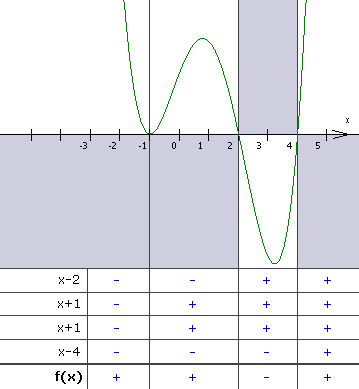Wir merken, dass es für jeden Faktor eine Nullstelle gibt, ab der er ins andere Vorzeichen umschlägt:

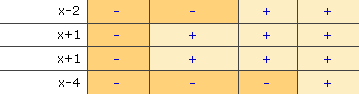Unzerlegbare Faktoren

Manchmal lässt sich die Funktion nicht vollständig in ihre Linearfaktoren zerlegen, wie z.B. bei

f(x) = (x – 3)·(x² + 1)

Wir können x² + 1 nicht weiter zerlegen, da diese Teilfunktion keine Nullstellen hat. In diesem Fall gilt die Funktion in der obigen Form bereits als bestmöglichst zerlegt. Auch beim Abstreichen der Vorzeichenfelder müssen wir den Faktor x² + 1 vollständig übernehmen:

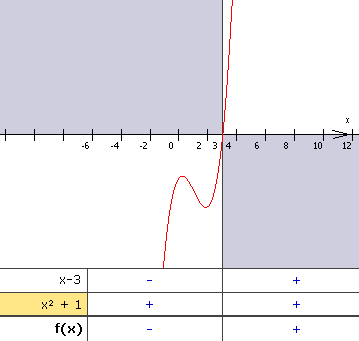Da sich unzerlegbare Teilfunktionen für jedes x entweder vollständig über oder vollständig unter der X-Achse befinden (sie besitzen keine Nullstellen, an denen sie ihr Vorzeichen wechseln könnten), haben sie entweder gar keinen Einfluss auf den Vorzeichenverlauf oder "drehen ihn um".

Eine Aufgabe zu diesem Kapitel wartet auf ihre Lösung!

Nächstes Kapitel:
2.3.3 Ableitung ganzrationaler Funktionen