5. Funktionsscharen

Funktionsscharen sind Funktionen mit einer weiteren Variablen (neben x) im Funktionsterm, z.B.:

fp(x) = x3 – p·x ;   p

Die Form des Graphen richtet sich nach gewähltem Parameter p, beispielsweise:

Bei der Kurvendiskussion von Funktionsscharen kan Werte immer nur in Abhängigkeit von p errechnen, z.B. die Nullstellen von f_p(x):

fp(x) = 0     x3 – p·x = 0;     x1 =     +       p             x2 =     –       p             x3 =     0

Wählt man z.B. p = 4, so hat die Funktion Nullstellen bei x = ± 2.

Kurven Parameter-abhängiger Punkte

Wir berechnen die Stelle der Terassenpunkte der Funktion j_k(x) in Abhängigkeit des Parameters k:

jk(x) = (x+k)3 + 1 + k     Wir untersuchen die Funktion und finden Terassenpunkte bei:     x = –k Tk(–k|k+1)

Nun wollen wir eine Kurve g(x) bestimmen, auf der jeder mögliche Terassenpunkt liegt, wenn man für k einen beliebigen Wert wählt:

Wir lösen die Gleichung x = –k nach k auf und setzen den Wert in f(–k) ein:     x = –k     k = –x  in  f(–k) = k + 1 einsetzen:         g(x) = –x + 1

Man sieht an der Zeichnung, dass tatsächlich alle Terassenpunkte auf g(x) = -x + 1 liegen:

Eine Aufgabe zu diesem Kapitel wartet auf ihre Lösung!

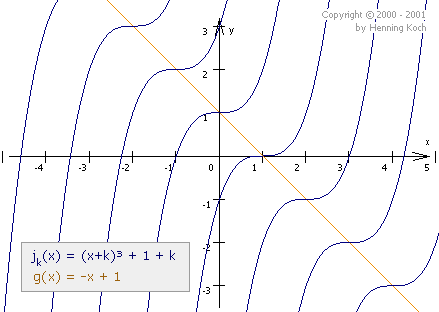Nächstes Kapitel:
6. Integration rationaler Funktionen