6. Integration rationaler Funktionen

Die Integration rationaler Funktionen wird üblicherweise erst in der Kollegstufe unterrichtet, und selbst da macht man Zugeständnisse an die Komplexität des Kapitels. Da die lückenlose Behandlung dieses Themas den Rahmen dieser Arbeit mehr als sprengen würde, soll hier nur ein praktisch orientierter Crash-Kurs in die Materie der bestimmten Integrale gegeben werden.

Was ist Integration?

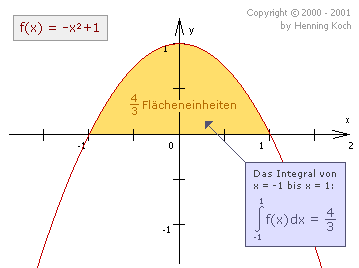
Bevor wir zu der praktischen Berechnung kommen, ein wenig vorab über Integration im allgemeinen. Integration ist in vielerlei Hinsicht die Umkehrung des Ableitens. Anschaulich gesehen kann man durch Integration die Fläche berechnen, die ein Funktionsgraph mit der X-Achse einschließt:

Dabei wird Fläche unterhalb der X-Achse als "negativ" gezählt, weshalb sich die Werte zweier Teilintegrale ganz oder teilweise aufheben können:

Man sagt auch, die Flächeninhalte sind orientiert. Will man den tatsächlichen, geometrischen Flächeninhalt eines Graphens berechnen, der sowohl unter und als auch über der X-Achse verläuft, so muss man erst die Nullstellen errechnen und abschnittsweise von Nullstelle zu Nullstelle integrieren. Den tatsächlichen Flächeninhalt erhält man dann, indem man die Beträge der einzelnen Teilintegrale aufaddiert.

Nächstes Kapitel:
6.1 Integration durch Stammfunktion