2.3.4 Monotonie

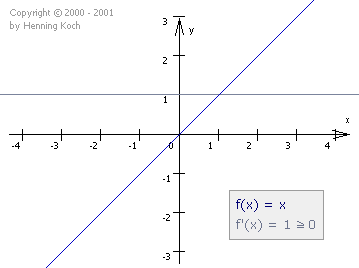
Eine Funktion f(x) heißt in einem Interval J monoton zunehmend, wenn der Graph von f(x) innerhalb von J ausschließlich steigt. Die Ableitungsfunktion f'(x), die ja die Steigung von f(x) angibt, muß also 0 innerhalb von J sein:

Analog heißt f(x) heißt monoton abnehmend, wenn der Graph innerhalb von J ausschließlich sinkt. Die Ableitungsfunktion f'(x) muß also 0 innerhalb von J sein:

Ist der Vorzeichenverlauf von f'(x) nicht auf Anhieb oder aus Erfahrungswert ersichtlich, kann man die Methode des Felderabstreichens auf f'(x) anwenden.

Strenge Monotonie

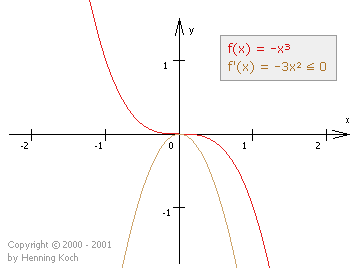
Spricht man von streng monoton zunehmend, bzw. abnehmend, so darf der Graph an keiner Stelle waagrecht verlaufen. Die Ableitungsfunktion f'(x) muss also durchwegs > 0, bzw. < 0 sein.

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
2.3.5 Lokale Extremwerte