2.3.6 Wendepunkte und Terrassenpunkte

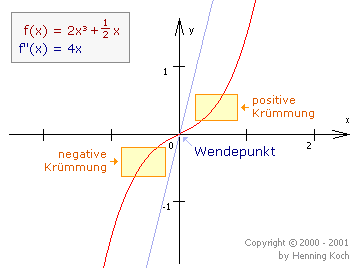
Man nennt einen Punkt auf dem Funktionsgraphen Wendepunkt, wenn an diesem Punkt die Krümmung vom Positiven ins Negative umschlägt, oder vom Negativen ins Positive. Extremwerte sind keine Wendepunkte, da dort die Krümmung sowohl vorher also auch nachher positiv (Minima), bzw. negativ (Maxima) ist:

Vorraussetzungen für einen Wendepunkt bei x₀ sind also:

1. f''(x₀) = 0
2. Vorzeichenwechsel von f''(x) bei x₀

Ist der Vorzeichenwechsel von f''(x) nicht auf Anhieb oder aus Erfahrungswert ersichtlich, kann man die Methode des Felderabstreichens auf f''(x) anwenden. In der Praxis setzt man auch oft geringfügig abweichende Werte (wie z.B. ± 0,01) links und rechts der fragwürdigen Stelle x₀ in f''(x) ein und vergleicht die Vorzeichen der beiden errechneten Werte.

Terrassenpunkte

Ist an einem so berechneten Wendepunkt zusätzlich noch f'(x₀) = 0, also die Tangente an der Stelle x₀ eine Waagrechte, so spricht man von einem speziellen Art von Wendepunkt, dem Terrassenpunkt:

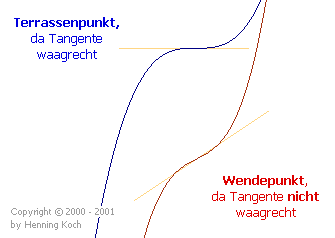Da sich an einem Terassenpunkt nach wie vor das Vorzeichen von f''(x) ändert, sind Terassenpunkte natürlich nach wie vor auch Wendepunkte.

Einige Aufgaben zu diesem Kapitel warten auf ihre Lösung!

Nächstes Kapitel:
2.3.7 Symmetrie des Graphen