Musteraufgabe und Zeichnung - Rationale Funktionen

3.9 Musteraufgabe und Zeichnung

Im folgenden werden wir eine Funktion nach allen in Kapitel 2.3 behandelten Gesichtspunkten untersuchen, und den Graphen am Ende auch zu Zeichnen versuchen.

Die Kurvendiskussion

Die gebrochenrationale Funktion, die wir untersuchen wollen lautet:

f(x) =
x³ + x² – x – 1

x² – x – 2

Symmetrie des Graphen

Wir errechnen f(-x):

f(–x) =
(–x)³ + (–x)² – (–x) – 1

(–x)² – (–x) – 2

f(–x) =

–x³ + x² + x – 1

x² + x – 2


f(–x) f(x)
f(–x) –f(x)

Die Funktion besitzt demnach kein Symmetrieverhalten bezüglich der Y-Achse oder dem Ursprung. Es kann durchaus ein anderes Symmetrieverhalten vorliegen, wir können es aber mit unseren Mitteln nicht feststellen. Wir können Symmetrie nur prüfen, nicht aufspüren.

Definitionslücken

Wir setzen die Nennerfunktion x² - x - 2 = 0 und erhalten als Lösungen:

x₁ = 2
x₂ = -1

Da kein unzerlegbarer Faktor übrigbleibt, können wir nun die Nennerfunktion vollständig in ihre Linearfaktoren zerlegt schreiben:

f(x) =
x³ + x² – x – 1

(x–2)(x+1)
= \ {–1; 2}

Nullstellen

Wir setzen die Zählerfunktion x³ + x² - x - 1 = 0 und erhalten als Lösungen:

x₃ = -1
x₄ = 1
x₅ = -1

Einzig ₄ = 1 ist im Definitionsbereich von f(x) enthalten, also hat die Funktion nur eine Nullstelle bei x = 1. Da kein unzerlegbarer Faktor übrigbleibt, können wir nun auch die Zählerfunktion vollständig in ihre Linearfaktoren zerlegt schreiben:

f(x) =
(x+1)(x–1)(x+1)

(x–2)(x+1)

Kürzen der Funktion

Der Faktor (x+1) ist sowohl im Zähler, als auch im Nenner vorhanden und lässt sich herauskürzen:

f(x) =
(x+1)(x–1)

(x–2)
= \ {–1; 2}

So umgeformt können wir am Funktionsterm und dem Definitionsbereich die Art der Definitionslücken ablesen:

Einfache Unendlichkeitsstelle bei x = 2
Definitionslücke ("Loch im Graphen") bei x = 1

Vorzeichenverlauf des Graphen

Um einen ungefähren Eindruck vom Verlauf des Graphens zu bekommen, streichen wir die Vorzeichenfelder ab:

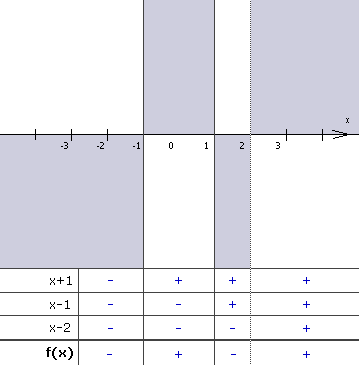Wir wissen nun, dass sich der Graph nicht in den ausgegrauten Feldern aufhalten kann.

Lokale Extremwerte

Zuerst bilden wir mit etwas Rechenaufwand die erste und zweite Ableitung f'(x) und f''(x). Natürlich dürfen wir dabei die gekürzte Fassung der Funktion ableiten!

f'(x) =
x² – 4x + 1

x² – 4x + 4

f''(x) =
6x – 12

x⁴ – 8x³ + 24x² – 32x + 16

Wir setzen f'(x) = 0 und erhalten als Lösungen:

x₆ = 2 +

3

3,73

x₇ = 2 –

3

0,27

Um zu überprüfen, ob es sich bei x₆ und x₇ wirklich um Extremwerte handelt, und wenn ja, ob es Minima oder Maxima sind, setzen wir die Werte in f''(x) ein:

f''(x₆) +5.29 > 0 Lokales Minimum bei x₆
f''(x₇) -1,15 < 0 Lokales Maximum bei x₇

Globale Extremwerte

Da die Funktion nicht nach oben oder unten beschränkt ist (einfache Unendlichkeitsstelle bei x = 2), macht die Bestimmung eines globalen Minimums und Maximums keinen Sinn.

Wendepunkte und Terassenpunkte

Wir setzen f''(x) = 0 und erhalten als Lösung x₈ = 2. Da jedoch sowohl der Zähler als auch der Nenner von f''(x) bei x = 2 sein Vorzeichen wechselt, wechselt f''(x) bei x = 2 sein Vorzeichen nicht. Die Funktion f(x) hat also auch keinen Wendepunkt bei x = 2.

Verhalten im Unendlichen

Der Grad des Zählerpolynoms von f(x) ist um eins höher als der des Nennerpolynoms. Die Funktion nähert sich also für große x an eine Gerade an. Die Funktionsgleichung dieser Grenzkurve (Asymptote) bekommen wir, indem wir mittels Polynomdivision Zähler durch Nenner dividieren:

f(x) =
(x+1)(x–1)

(x–2)
   =
x² – 1

x – 2
   = x + 2 +
3

x – 2
   ;
Wir erkennen das letzte Glied des Termes, das für unendlich große x zu Null wird:
x + 2 +
3

x – 2
   =
x + 2

Die Gleichung der Grenzkurve lautet also k(x) = x + 2.

Die qualitative Zeichnung

Wir zeichnen wieder alle bekannten Eigenschaften der Funktion f(x) in ein Koordinatensystem, wenn möglich in dasselbe, in dem zuvor bereits die Vorzeichenfelder abgestrichen wurden. Um die Y-Koordinaten der Extremwerte, Wendepunkte, etc. zu erhalten, setzt man sie einfach in f(x) ein:

Wenn man den Graphen genauer zeichnen möchte, kann man noch zusätzlich einzelne Funktionswerte ausrechnen und in das Koordinatensystem einzeichnen. Besonders der Funktionswert bei x = 0 (der Y-Achsen-Abschnitt) ist schnell auszurechnen und bei der Zeichnung äußerst hilfreich. Schließlich haben wir genug Informationen, um den Graphen in das Koordinatensystem hineinskizzieren zu können:

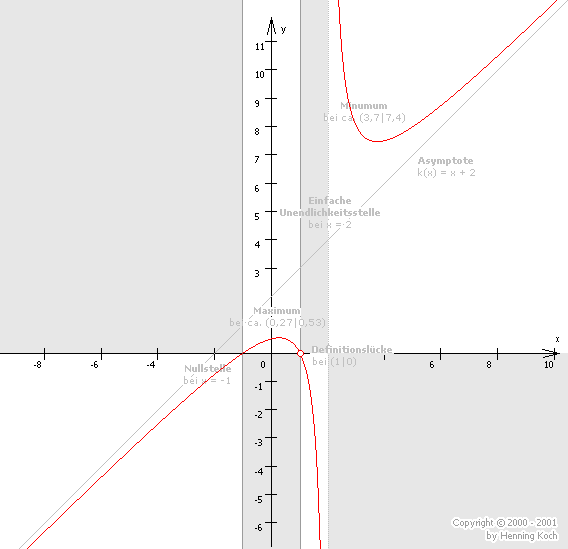Eine Aufgabe zu diesem Kapitel wartet auf ihre Lösung!

Nächstes Kapitel:
3.10 Schlußbemerkung zu den gebrochenrationalen Funktionen