Kurvendiskussion und Musteraufgabe - Rationale Funktionen

4.5 Kurvendiskussion und Musteraufgabe

Bei der Kurvendiskussion abschnittsweise definierter Funktionen muss man tatsächlich alle Teilfunktionen getrennt voneinander untersuchen, unter Berücksichtigung des jeweiligen Definitionsbereiches.

Beispiel

Wir wollen die folgende Funktion f(x) auf Nullstellen, Extremwerte und Wendepunkte hin untersuchen. Zur besseren Übersicht in der Rechnung später haben wir die einzelnen Teilfunktionen mit j(x), k(x) und l(x) benannt:

f(x) =
j(x) = x + 3 = [–3;–2[
k(x) = –x² = [–2;2]
l(x) = x – 1 = ]2;3]

= [–3;3]

Da f(x) aus recht einfachen Teilfunktionen zusammengesetzt ist, können wir den Graphen der Funktion sofort ohne große Probleme zeichen:

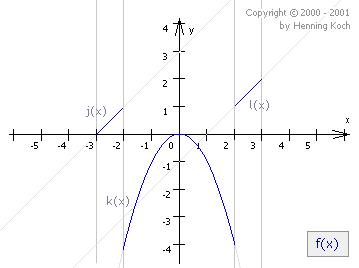Der Graph ist zwar zur Kurvendiskussion nicht notwendig, eignet sich jedoch hervorragend dazu, Ergebnisse anschaulich zu überprüfen.

Symmetrie

Zur Symmetrie von f(x) müssten alle Teilfunktionen eine Symmetrie besitzen. Da jedoch bereits
j(x) weder spiegelsymmetrisch zur Y-Achse, noch punktsymmetrisch zum Ursprung ist, gilt das selbe für f(x).

Stetigkeit auf

Jede der Teilfunktionen ist eine rationale Funktion und ist damit auf ihrem jeweiligen Definitionsbereich stetig. Wir betrachten nun noch die Grenzen zwischen den Intervallen der Teilfunktionen: Da
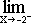f(x) 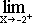f(x) und auch f(x) f(x) reißt die Funktion an gleich zwei Stellen ab und ist damit auf nicht stetig.

Nullstellen

Um die Nullstellen f(x) zu berechnen, müssen wir die Nullstellen von j(x), k(x) und l(x) berechnen:

j(x) = 0 x + 3 = 0
x₁ = -3
k(x) = 0 -x² = 0
x₂ = 0
l(x) = 0 x - 1 = 0
x₃ = 1

x₁ und x₂ sind also Nullstellen von f(x). x₃ hingegen ist keine Nullstelle von f(x), da x₃ nicht im Definitionsbereich der Teilfunktion l(x) enthalten ist:

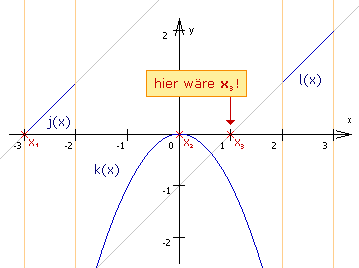Lokale Extremwerte

Wir leiten f(x) zu f'(x) und f''(x) ab. Man achte auf die Intervallgrenzen der Definitionsbereiche. Wie bereits behandelt sind die Intervallgrenzen nach einer Ableitung nie enthalten:

f'(x) =
j'(x) = 1 = ]–3;–2[
k'(x) = –2x = ]–2;2[
l'(x) = 1 = ]2;3[

f''(x) =
j''(x) = 0 = ]–3;–2[
k''(x) = –2 = ]–2;2[
l''(x) = 0 = ]2;3[

Zur Berechnung der lokale Extremwerte setzen wir f'(x) = 0 und stellen wenn möglich über f''(x) die Art des Extremums fest:

j'(x) = 0;
1 0; (keine Lösung)
k'(x) = 0;
-2x = 0;
x₄ = 0
f''(0) = -2
lokales Maximum bei x = 0
l'(x) = 0;
1 0; (keine Lösung)

Die Funktion f(x) hat also ein lokales Maximum bei P₄(0|0). Da f(x) an den Grenzen zwischen den Intervallen der Teilfunktionen nicht stetig ist, kann sie dort auch keine lokalen Randextrema besitzen.

Globale Extremwerte

Da die Funktion nirgends nach + oder - strebt, ist sie sowohl nach oben, als auch nach unten begrenzt:

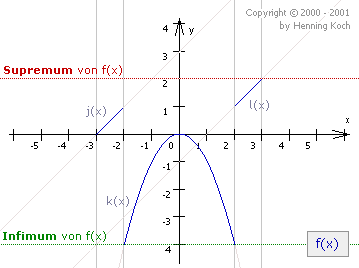Es kann also nach globalen Extremwerten gesucht werden. Wir haben bereits ein lokales Maximum bei P₄(0|0) gefunden, und vergleichen jetzt dessen Funktionswert (y = 0) mit den Funktionswerten an den Abschnittsrändern:

f(x) =
j(x) = x + 3; = [–3;–2[
f(–3) = 0; (linke Seite von )
f(x) = 1 (rechte Seite von )
k(x) = –x² = [–2;2]
f(–2) = –4; (linke Seite von )
f(2) = –4; (rechte Seite von )

l(x) = x – 1 = ]2;3]
f(x) = 1 (linke Seite von )
f(3) = 2 (rechte Seite von )

Das globale Maximum der Funktion f(x) ist also bei P₅(3|2), das globale Minimum bei P₆(-2|-4) oder P₇(2|-4). P₅, P₆ und P₇ sind alles Randextrema!

Wendepunkte, Terassenpunkte

Da f''(x) keinen Vorzeichenwechsel hat (eine der Bedingungen für einen Wende- oder Terassenpunkt), kann f(x) auch keine Wende- oder Terassenpunkte besitzen.

Eine Aufgabe zu diesem Kapitel wartet auf ihre Lösung!

Nächstes Kapitel:
4.6 Beträge im Funktionsterm